This seems to be one of the most popular questions faced by statisticians, and one that, although may seem simple, always requires additional information. Let's say we are designing a study to investigate if there is a statistically significant difference between the average performance of two populations, like the average mpg of two types of cars, or the average DC resistance of two cable designs. In this two-sample test of significance scenario the sample size calculation depends on four "ingredients":
1. The smallest difference between the two averages that we want to be able to detect
2. The estimate of the standard deviation of the two populations
3. The probability of declaring that there is a difference when there is none
4. The probability of detecting a difference when the difference exists
The third ingredient is known as the significance level of the test, and is the probability of making a Type I error; i.e., declaring that there is a difference between the populations when there is none. The value of the significance level (Alpha) is usually taken as 5%. It was
Sir Ronald Fisher, one of the founding fathers of modern statistics, who suggested the value of 0.05 (1 in 20)
as a limit in judging whether a deviation ought to be considered significant or not.
However, I do not believe Fisher intended 5% to become the default value in tests of significance. Notice what he wrote in his 1956 book Statistical Methods and Scientific Inference.
No scientific worker has a fixed level of significance from year to year, and in all circumstances, he rejects hypothesis; he rather gives his mind to each particular case in the light of his evidence of ideas. (3rd edition, Page 41)
The last ingredient reflects the ability of the test to detect a difference when it exists; i.e. its power. We want our studies to have good power, a suggested value is 80%. But be careful, the more power you want the more samples you are going to need. In a future post I will show you how a Sample Size vs. Power plot is a great tool to evaluate how many samples are needed to achieve certain power.
The research hypothesis under consideration should drive the sample size calculations. Let's say that we want to see if there is a difference in the the average DC resistance performance of two cable designs. Given that the standard deviation for these cable designs is about 0.5 Ohm, the question of "how many samples do we need?" now becomes:
how many samples do we need to be able to detect a difference of at least 1 Ohm between the two cable designs, with a significance level of 5% and a power of 80%.
In JMP it is very easy to calculate sample sizes as a function of the four ingredients described above. From the DOE menu select Sample Size and Power, and then the type of significance test to be performed. The figure below shows the Sample Size and Power dialog window for the DC resistance two-sample test of significance. Note that by default JMP populates Alpha, the significance level of the test, with 0.05. The highlighted values are the required inputs and the "Sample Size" the total required sample size for the study.
The results indicate that we need about 11 samples, or 6 per cable design, to be able to detect a difference of at least 1 Ohm between the two cable designs.
Next time you ask yourself, or your local statistician, how many samples are needed, remember that additional information is required, and that the calculations only tell you how many samples you need but not how and where to take the samples, the sampling scheme (more about sampling schemes on a future post).
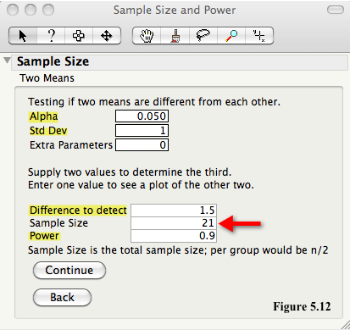In my previous post, How Many Do I Need?, I went over the required four "ingredients" for the calculations. We use JMP's default value of Alpha= 0.05 (5%), as the significance level for the test, we state that the noise in the system Std Dev=1 unit, or 1 sigma, that we want to detect a difference of at least 1.5 standard deviations (Difference to detect), and that we want the test to have Power of 0.9 (90%). The calculator indicates that we need a total of 21 samples, or 21/2 = 11 (rounding up) per group, for our study. 
