Tolerance (Coverage) Intervals

You are probably familiar with confidence intervals as a way to place bounds, with a given statistical confidence, on the parameters of a distribution. In my post I Am Confident That I Am 95% Confused!, I used the DC resistance data shown below to illustrate confidence intervals and the meaning of confidence.

From the JMP output we can see that the average resistance for the sample of 40 cables is 49.94 Ohm and that, with 95% confidence, the average DC resistance can be as low as 49.31 Ohm, or as large as 50.57 Ohm. We can also compute a confidence interval for the standard deviation. That's right, even the estimate of noise has noise. This is easily done by selecting Confidence Interval > 0.95 from the contextual menu next to DC Resistance

We can say that, with 95% confidence, the DC resistance standard deviation can be as low as 1.61 Ohm, or as large as 2.52 Ohm.

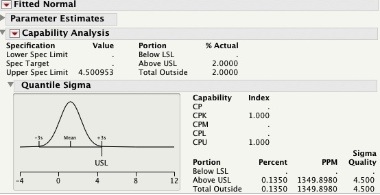
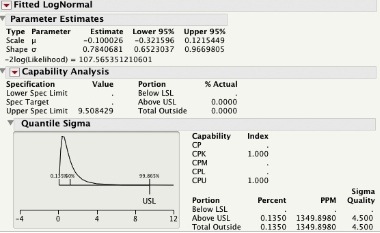
Although confidence intervals have many uses in engineering and scientific applications, a lot of times we need bounds not on the distribution parameters but on an given proportion of the population. In her post, 3 Is The Magic Number, Brenda discussed why the mean ± 3×(standard deviation) formula is popular for setting specifications. For a Normal distribution, if we know the mean and standard deviation without error, we expect about 99.73% of the population to fall within mean ± 3×(standard deviation). In fact, for any distribution the Chebyshev's inequality guarantees that 88.89% of the population will be contained between ± 3×standard deviations. It gets better. If the distribution is unimodal we expect at least 95.06% of the population to be between ± 3×standard deviations.

In real applications, however, we seldom know the mean and standard deviation without error. These two parameters have to be estimated from a random and, usually small, representative sample. A tolerance interval is a statistical coverage interval that includes at least a given proportion of the population. This type of interval takes into account both the sample size and the noise in the estimates of the mean and standard deviation. For normally distributed data an approximate two-sided tolerance interval is given by

Here g(1-α/2,p,n) takes the place of the magic "3", and is a function of the confidence,1-α/2, the proportion that we want the interval to cover (you can think of this as the yield that we want to bracket), p, and the sample size n. These intervals are readily available in JMP by selecting Tolerance Interval within the Distribution platform, and specifying the confidence and the proportion of the population to be covered by the interval.

For the DC resistance data the mean ± 3×(standard deviation) interval is 49.94±3×1.96 = [44.06 Ohm;55.82 Ohm], while the 95% tolerance interval to cover at least 99.73% of the population is [42.60 Ohm;57.28 Ohm]. The tolerance interval is wider than the mean ± 3×(standard deviation) interval, because it accounts for the error in the estimates of the mean and standard deviation, and the small sample size. Here we use a coverage of 99.73% because this is what is expected between ± 3×standard deviations, if we knew the mean and sigma.

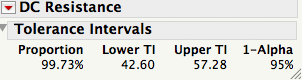
Tolerance intervals are a great practical tool because they can be used to set specification limits, as surrogate for specification limits, or to compare them to a given set of specification limits; e.g., from our customer, to see if we will be able to meet them.

To "Log" or Not to "Log"

Many statistical techniques rely upon the assumption that the data follows a normal distribution. In fact, questions surrounding the impact of normality on the validity of a statistical analysis ranks right up there with 'how many samples do I need for my results to be meaningful?'. Some statistical techniques derived from an assumption of normality of the data can deal with slight to moderate departures quite well, while others are greatly impacted. For instance, if a response such as bond strength is slightly skewed to the right with a mean well above 0 then a control chart for subgroup averages derived in the typical manner, using 3 sigma limits, should have adequate performance in detecting a large shift in the mean. However, a response which is heavily skewed to the right, with a lower boundary close to 0, for example, will produce unreasonable results using techniques based upon normality.

Let's examine the impact of departures from normality when setting a '3 sigma' upper specification limit based upon process capability, for a response that inherently follows a lognormal distribution. In the figure below, we see a histogram for 50 measurements of a response, which was randomly generated using a lognormal distribution. At first glance it is obvious that the distribution is skewed to the right with a lower bound close to 0, putting the normality assumption in question. However, is it so skewed that it will call into question the accuracy of statistical techniques derived from a normal assumption?

Let's fit a normal distribution to the data and use the normal probability model to determine the value at which the probability of exceeding it is 0.135%, i.e., a '3 sigma' equivalent upper limit. This value is 4.501, with 2% of the actual readings above this upper limit.

Now, let's fit the more appropriate lognormal distribution to this data and use the lognormal probability model to determine the value at which the probability of exceeding it is 0.135%, i.e., a '3 sigma' equivalent upper limit. This value is 9.501, with no actual readings above this limit.

The upper limits derived from these two distributions are quite different from each other; 9.501 (lognormal) vs. 4.501 (normal). Since we know this response is lognormal, we would be significantly underestimating the '3 sigma' upper limit using the normal assumption, resulting in 2% out-of-spec readings, compared to 0.135% that we set out to achieve. In a real world application, this could result in chasing false alarms on a control chart or scrapping product that is well within the distribution of the data. Before moving forward with a statistical analysis of your data, determine the best fitting distribution by evaluating the histogram, distribution based quantile plots, goodness of fit tests, and most importantly, understanding the context of the data. The best distributions to use for many engineering and scientific applications are well known and well documented.