Effective Sample Size

It is Monday morning and you are traveling from home to work, a 20 miles journey, when you hit a traffic jam. Things are slow, traffic is doing about 20 mph; you start getting anxious about that meeting they scheduled for 8. After 10 miles of slow traffic the road suddenly clears up and you decide to travel the remaining 10 miles at a speed of 80 mph. You are late to the meeting and tell your boss what happened, she listen quietly and asks, what was your average speed?

Some people, when they hear the word average, automatically think of adding the two numbers, 20+80, and dividing the result by 2. The arithmetic mea of these two speeds is 50 mph. However, miles per hour (mph) is a ratio of two quantities for which the arithmetic average is not appropriate. The first 10 miles, traveling @20 mph, took you 30 minutes, while the last 10 miles, traveling @80 mph, took you 7.5 minutes. Since you traveled 20 miles in 37.5 minutes your average speed is 20*(60/37.5) = 32 mph.

The "average" of these two speeds is given not by the arithmetic mean but by the harmonic mean: the product of the two numbers divided by the arithmetic average of the two. The "average" speed is then [20x80] / [(20+80)/2] = 32. In general, for a set of n positive numbers, the harmonic mean H resembles the arithmetic average but in an inverted sort of way,

The harmonic mean is useful for determining the effective sample size when comparing two populations means. This is because the precision of the average, X̄, is given by the standard deviation, which is inversely related to the sample size. The effective sample size for comparing two means with sample sizes n₁ and n₂ is given by

Let's say you are conducting a study two compare two products, A and B, using a two-sample t-test, and you take a random sample of 4 product A, and a random sample of 12 product B units (since you want to be "sure" about product B you take "extra" samples). The effective sample size for comparing the average of the 4 product A samples with the average of the 12 product B samples is then [4x12]/[(4+12)/2] = 6. What this means is that your study with 16 samples is equivalent to a study with 6 samples each from populations A and B, for a total of 12 samples. In other words, you are using 4 extra samples.

As you can see, having a balanced number of samples (n₁=n₂) per population is not just a statistical nicety, but can save you materials, time, and money.

Statistics Is the New Grammar

That is how Clive Thompson ends his article Do You Speak Statistics? in the May issue of Wired magazine. I like this sentence, it makes you think of statistics in a different way. Grammar has to do with language, with syntax, or "the principles or rules of an art, science, or technique" (Merriam-Webster). Statistics being the "New Grammar" implies a language that we may not totally understand, or even be aware of: a new way of looking at, and interpreting the world around us. Through several examples Thompson makes the point that statistics is crucial for public life.

…our inability to grasp statistics — and the mother of it all, probability — makes us believe stupid things. (Clive Thompson)

Back in the late 80s Prof. John A. Paulos wrote a book Innumeracy: Mathematical Illiteracy and Its Consequences, using a term, innumeracy, coined by Prof. Douglas R Hofstadter to denote a "person's inability to make sense of numbers" (Thompson quotes Prof. Allen but it does not mention innumeracy). In my post Lack of Statistical Reasoning I wrote about Prof. Pinker's observation that lack of statistical reasoning is the most important scientific concept that lay people fail to understand. When someone asks me what I do for a living I tell them that I help people "make sense of data", and when I collaborate with, and teach, engineers and scientists I help them realize what may seem obvious:

variation exists in everything we do;
understanding and reducing variation is key for success.

Thompson argues that "thinking statistically is tricky". Perhaps, but Statistical Thinking starts with the realization that, as Six-Sigma practitioners know full well, variation is everywhere.

A lot of controversy has been generated after the hacking of emails of the Climatic Research Unit (CRU) at the University of East Anglia. The university set up a Scientific Appraisal Panel to "assess the integrity of the research published by the Climatic Research Unit in the light of various external assertions". The first conclusion of the report is "no evidence of any deliberate scientific malpractice in any of the work of the Climatic Research Unit". From the statistics point of view is very interesting to read the second conclusion:

We cannot help remarking that it is very surprising that research in an area that depends so heavily on statistical methods has not been carried out in close collaboration with professional statisticians.

The panel's opinion is that the work of the scientists doing climate research "is fundamentally statistical", echoing Thompson's argument.

A few years ago Gregory F. Treverton, Director, RAND Center for Global Risk and Security, wrote an interesting article, Risks and Riddles, where he made a wonderful distinction between puzzles and mysteries: "Puzzles can be solved; they have answers", "A mystery cannot be answered; it can only be framed". But the connection he made between puzzles and mysteries to information is compelling,

Puzzle-solving is frustrated by a lack of information.
By contrast, mysteries often grow out of too much information. (Gregory F. Treverton)

There is so much information these days that another Wired magazine writer, Chris Anderson, calls it the Petabyte Age. A petabyte is a lot of data, a petabyte is a quadrillion bytes (10¹⁵), or the equivalent to about 13 years of HD-TV video. Google handles so much information that in 2008 was processing over 20 petabytes of data per day. In this data deluge, how do we know what to keep (signal) and what to throw away (noise)? That is why statistics is the new grammar.

What If Einstein Had JMP?

Last week I had the opportunity to speak at the third Mid-Atlantic JMP Users Group (MAJUG) conference, hosted by the University of Delaware in Newark, Delaware (UDaily). The opening remarks were given by the Dean of the College of Engineering, Michael Chajes, who used the theme of the event, "JMP as Catalyst for Engineering and Science", to emphasize that the government and the general public need to realize that science alone is not enough for the technological advances that are required in the future, we also need engineering. It was a nice lead to my opening slide, the quote by Theodore Von Karman:

Scientists discover the world that exists;
engineers create the world that never was.

I talked about some of the things that made Einstein famous (traveling on a beam of light, turning off gravity, mass being a form of energy), as well as some things that may not be well known. Do you know that he used statistics in his first published paper, Conclusions Drawn from the Phenomena of Capillarity (Annalen der Physik 4 (1901), 513-523)?

Einstein "started from the simple idea of attractive forces amongst the molecules", which allowed him to write the relative potential of two molecules, assuming they are the same, as a sum of all pair interactions P = P_∞ - ½ c² ∑∑φ(r). In this equation "c is a characteristic constant of the molecule, φ(r), however, is a function of the distance of the molecules, which is independent of the nature of the molecule". "In analogy with gravitational forces", he postulated that the constant c is an additive function of the number of atoms in the molecule; i.e., c =∑c_α, giving a further simplification for the potential energy per unit volume as P = P_∞ - K(∑c_α)²/ν². In order to study the validity of this relationship Einstein "took all the data from W. Ostwald's book on general chemistry", and determined the values of c for 17 different carbon (C), hydrogen (H), and oxygen (O) molecules.

It is interesting that not a single graph was provided in the paper. Had he had JMP he could have used my favorite tool, the graphics canvas of the graph builder, to display the relationship between the constant c and the number of atoms in each of the elements in the molecule.

We can clearly see that c increases linearly with the number of atoms in C and H (the last point, corresponding to the molecule with 16 hydrogen atoms, seems to fall off the line), but not so much with the number of oxygen atoms. We can also see that for the most part, the 17 molecules chosen have more hydrogen atoms than carbon atoms, and carbon atoms than oxygen atoms. This "look test", as my friend Jim Ford calls it, is the catalyst that can spark new discoveries, or the generation of new hypotheses about our data.

In order to find the fitting constant in the linear equation c =∑c_α, he "used for the calculation of c_α for C, H, and O [by] the least squares method". Einstein was clearly familiar with the method and, as Iglewicz (2007) puts it, this was "an early use of statistical arguments in support of a scientific proposition". These days it is very easy for us to fit a linear model using least squares. We just "add" the data to JMP and with a few clicks voilà, we get the "fitting constants", or parameter estimates as we statisticians call them, of our linear equation.

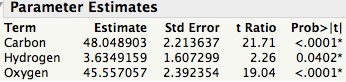
For a given molecule we can, using the parameter estimates from the above table, write the constant c = 48.05×#Carbon Atoms + 3.63×#Hydrogen Atoms + 45.56×#Oxygen Atoms.

For young Einstein it was another story. Calculations had to be done by hand, and round off and arithmetic errors produced some mistakes. Iglewicz notes "simple arithmetic errors and clumsy data recordings, including use of the floor function rather than rounding". He also didn't have available the wealth of regression diagnostics that have been developed to assess the goodness of the least squares fit. JMP provides many of them within the "Save Columns" menu.

One the first plots we should look at is a plot of the studentized residuals vs. predicted values. Points that scatter around the zero line like "white noise" are an indication that the model has done a good job at extracting the signal from the data leaving behind just noise. For Einstein's data the studentized residuals plot clearly shows a no so "white noise" pattern, putting into question the adequacy of the model. Points beyond ±3 in the y axis, are a possible indication of response "outliers". Note that two points are more than 2 units away from 0 center line. One of them corresponds to the high hydrogen point that we saw in the graph builder plot.

In addition to the studentized residuals and predicted values there are two diagnostics, the Hats (leverage) and the Cook's D Influence, that are particularly useful for determining if a particular observation is influential on the fitted model. A high Hat value indicates a point that is distant from the center of the independent variables (X outliers), while a large Cook's D indicates an influential point, in the sense that excluding from the fit may cause changes in the parameter estimates.

A great way to combine the studentized residuals, the Hats, and the Cook's D is by means of a bubble plot. We plot the studentized residuals on the Y-axis, the Hats on the X-axis, and use the Cook's D to define the size of the bubble. We overlay a line at 0 in the Y-axis, to help the eye assess randomness and gauge distances from 0, and a line at 2×3/17 ≃ 0.35 in the X-axis, to assess how large the Hats are. Here 3 is the number of parameters or "fitting constants" in the model and 17 corresponds to the number of observations.

Right away we can see that molecule #1, Limonene, the one with the largest number of hydrogen atoms (16), is a possible outlier in both the Y (studentized residual=-3.02) and X (Hat=0.47), and also and influential observation (Cook's D=1.99). Molecule #16, Valeraldehyde, could also be an influential observation. What to do? One can fit the model without Limonene and Valeraldehyde to study their effect on the parameter estimates, or perhaps consider a different model.

In the final paragraph of his paper Einstein notes that "Finally, it is noteworthy that the constants c_α in general increase with increasing atomic weight, but not always proportionally", and goes on to explain some of the questions that need further investigation, pointing out that ‘We also assume that the potential of the molecular forces is the same as if the matter were to be evenly distributed in space. This, however, is an assumption which we can expect to be only approximately true." Murrell and Grobert (2002) indicate that this is a very poor approximation because it "greatly overestimate the attractive forces" between the molecules.

For more on Einstein first published paper you can look at the papers by Murrell and Grobert (2002) and Iglewicz (2007), and Chapter 7 of our book Analyzing and Interpreting Continuos Data Using JMP where we analyze Einstein's data in more detail.
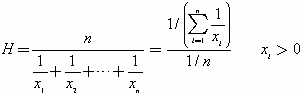